Associated Readings adapted from Think Python - How To Think Like A Computer Scientist by Allen Downey

Unit 1

1.1

Values and Types

A value is one of the basic things a program works with, like a letter or a number. The values we have seen so far are 1, 2, and 'Hello, World!'.

These values belong to different types: 2 is an integer, and 'Hello, World!' is a string, so-called because it contains a “string” of letters. You (and the interpreter) can identify strings because they are enclosed in quotation marks.

If you are not sure what type a value has, the interpreter can tell you.

>>> type('Hello, World!')
<type 'str'>

>>> type(17)
<type 'int'>

Not surprisingly, strings belong to the type str and integers belong to the type int. Less obviously, numbers with a decimal point belong to a type called float, because these numbers are represented in a format called floating-point.

>>> type(3.2)
<type 'float'>

What about values like '17' and '3.2'? They look like numbers, but they are in quotation marks like strings.

>>> type('17')
<type 'str'>
>>> type('3.2')
<type 'str'>

They’re strings. When you type a large integer, you might be tempted to use commas between groups of three digits, as in 1,000,000. This is not a legal integer in Python, but it is legal:

>>> 1,000,000
(1, 0, 0)

Well, that’s not what we expected at all! Python interprets 1,000,000 as a comma-separated sequence of integers. This is the first example we have seen of a semantic error: the code runs without producing an error message, but it doesn’t do the “right” thing.

Operators and Operands

Operators are special symbols that represent computations like addition and multiplication. The values the operator is applied to are called operands.

The operators +, -, , / and * perform addition, subtraction, multiplication, division and exponentiation, as in the following examples:

20+32 hour-1 hour60+minute minute/60 5**2 (5+9)(15-7) In some other languages, ^ is used for exponentiation, but in Python it is a bitwise operator called XOR. We won’t cover bitwise operators in this book, but you can read about them at http://wiki.Python.org/moin/BitwiseOperators. Exponentiation in Python3 is **. In Python 3, the division operator might not do what you expect:

>>> minute = 59
>>> minute/60
0

The value of minute is 59, and in conventional arithmetic 59 divided by 60 is 0.98333, not 0. The reason for the discrepancy is that Python is performing floor division. When both of the operands are integers, the result is also an integer; floor division chops off the fraction part, so in this example it rounds down to zero. In Python 3, the result of this division is a float. The new operator // performs floor division.

If either of the operands is a floating-point number, Python performs floating-point division, and the result is a float:

>>> minute/60.0
0.98333333333333328

Expressions and Statements

An expression is a combination of values, variables, and operators. A value all by itself is considered an expression, and so is a variable, so the following are all legal expressions (assuming that the variable x has been assigned a value):

17
x
x + 17

A statement is a unit of code that the Python interpreter can execute. We have seen two kinds of statement: print and assignment. Technically an expression is also a statement, but it is probably simpler to think of them as different things. The important difference is that an expression has a value; a statement does not.

1.2

Variables

One of the most powerful features of a programming language is the ability to manipulate variables. A variable is a name that refers to a value.

An assignment statement creates new variables and gives them values:

>>> message = 'And now for something completely different'
>>> n = 17
>>> pi = 3.1415926535897932

This example makes three assignments. The first assigns a string to a new variable named message; the second gives the integer 17 to n; the third assigns the (approximate) value of π to pi. A common way to represent variables on paper is to write the name with an arrow pointing to the variable’s value. This kind of figure is called a state diagram because it shows what state each of the variables is in (think of it as the variable’s state of mind). Figure 2.1 shows the result of the previous example.

The type of a variable is the type of the value it refers to.

>>> type(message)
<type 'str'>
>>> type(n)
<type 'int'>
>>> type(pi)
<type 'float'>

Variable names and keywords

Programmers generally choose names for their variables that are meaningful—they document what the variable is used for.

Variable names can be arbitrarily long. They can contain both letters and numbers, but they have to begin with a letter. It is legal to use uppercase letters, but it is a good idea to begin variable names with a lowercase letter (you’ll see why later).

The underscore character, _, can appear in a name. It is often used in names with multiple words, such as my_name or airspeed_of_unladen_swallow.

If you give a variable an illegal name, you get a syntax error:

>>> 76trombones = 'big parade'
SyntaxError: invalid syntax
>>> more@ = 1000000
SyntaxError: invalid syntax
>>> class = 'Advanced Theoretical Zymurgy'
SyntaxError: invalid syntax

76trombones is illegal because it does not begin with a letter. more@ is illegal because it contains an illegal character, @. But what’s wrong with class?

It turns out that class is one of Python’s keywords. The interpreter uses keywords to recognize the structure of the program, and they cannot be used as variable names.

Python 2 has 31 keywords:

and       del       from      not       while
as        elif      global    or        with
assert    else      if        pass      yield
break     except    import    print
class     exec      in        raise
continue  finally   is        return
def       for       lambda    try

In Python 3, exec is no longer a keyword, but nonlocal is. You might want to keep this list handy. If the interpreter complains about one of your variable names and you don’t know why, see if it is on this list.

1.3

What is debugging?

Programming is error-prone. For whimsical reasons, programming errors are called bugs and the process of tracking them down is called debugging.

Three kinds of errors can occur in a program: syntax errors, runtime errors, and semantic errors. It is useful to distinguish between them in order to track them down more quickly.

Syntax errors

Python can only execute a program if the syntax is correct; otherwise, the interpreter displays an error message. Syntax refers to the structure of a program and the rules about that structure. For example, parentheses have to come in matching pairs, so (1 + 2) is legal, but 8) is a syntax error.

In English, readers can tolerate most syntax errors, which is why we can read the poetry of e. e. cummings without spewing error messages. Python is not so forgiving. If there is a single syntax error anywhere in your program, Python will display an error message and quit, and you will not be able to run your program. During the first few weeks of your programming career, you will probably spend a lot of time tracking down syntax errors. As you gain experience, you will make fewer errors and find them faster.

Runtime errors

The second type of error is a runtime error, so called because the error does not appear until after the program has started running. These errors are also called exceptions because they usually indicate that something exceptional (and bad) has happened.

Runtime errors are rare in the simple programs you will see in the first few chapters, so it might be a while before you encounter one.

Semantic errors

The third type of error is the semantic error. If there is a semantic error in your program, it will run successfully in the sense that the computer will not generate any error messages, but it will not do the right thing. It will do something else. Specifically, it will do what you told it to do.

The problem is that the program you wrote is not the program you wanted to write. The meaning of the program (its semantics) is wrong. Identifying semantic errors can be tricky because it requires you to work backward by looking at the output of the program and trying to figure out what it is doing.

Experimental debugging

One of the most important skills you will acquire is debugging. Although it can be frustrating, debugging is one of the most intellectually rich, challenging, and interesting parts of programming. In some ways, debugging is like detective work. You are confronted with clues, and you have to infer the processes and events that led to the results you see.

Debugging is also like an experimental science. Once you have an idea about what is going wrong, you modify your program and try again. If your hypothesis was correct, then you can predict the result of the modification, and you take a step closer to a working program. If your hypothesis was wrong, you have to come up with a new one. As Sherlock Holmes pointed out, “When you have eliminated the impossible, whatever remains, however improbable, must be the truth.” (A. Conan Doyle, The Sign of Four)

For some people, programming and debugging are the same thing. That is, programming is the process of gradually debugging a program until it does what you want. The idea is that you should start with a program that does something and make small modifications, debugging them as you go, so that you always have a working program.

For example, Linux is an operating system that contains thousands of lines of code, but it started out as a simple program Linus Torvalds used to explore the Intel 80386 chip. According to Larry Greenfield, “One of Linus’s earlier projects was a program that would switch between printing AAAA and BBBB. This later evolved to Linux.” (The Linux Users’ Guide Beta Version 1).

Unit 2

2.1 Variables, expressions and statements

Values and types

A value is one of the basic things a program works with, like a letter or a number. The values we have seen so far are 1, 2, and 'Hello, World!'.

These values belong to different types: 2 is an integer, and 'Hello, World!' is a string, so-called because it contains a “string” of letters. You (and the interpreter) can identify strings because they are enclosed in quotation marks.

If you are not sure what type a value has, the interpreter can tell you.

>>> type('Hello, World!')
<type 'str'>
>>> type(17)
<type 'int'>

Not surprisingly, strings belong to the type str and integers belong to the type int. Less obviously, numbers with a decimal point belong to a type called float, because these numbers are represented in a format called floating-point.

>>> type(3.2)
<type 'float'>
What about values like '17' and '3.2'? They look like numbers, but they are in quotation marks like strings.
>>> type('17')
<type 'str'>
>>> type('3.2')
<type 'str'>

They’re strings. When you type a large integer, you might be tempted to use commas between groups of three digits, as in 1,000,000. This is not a legal integer in Python, but it is legal:

>>> 1,000,000
(1, 0, 0)

Well, that’s not what we expected at all! Python interprets 1,000,000 as a comma-separated sequence of integers. This is an example we have seen of a semantic error: the code runs without producing an error message, but it doesn’t do the “right” thing.

Exercises

Exercise 1

Assume that we execute the following assignment statements:

width = 17
height = 12.0
delimiter = '.'

For each of the following expressions, write the value of the expression and the type (of the value of the expression).

• width/2
• width/2.0
• height/3
• 1 + 2 * 5
• delimiter * 5

Use the Python interpreter to check your answers.

Exercise 2

Practice using the Python interpreter as a calculator:

The volume of a sphere with radius r is 4/3 π r3. What is the volume of a sphere with radius 5? Hint: 392.7 is wrong! Suppose the cover price of a book is $24.95, but bookstores get a 40% discount. Shipping costs $3 for the first copy and 75 cents for each additional copy. What is the total wholesale cost for 60 copies?

If I leave my house at 6:52 am and run 1 mile at an easy pace (8:15 per mile), then 3 miles at tempo (7:12 per mile) and 1 mile at easy pace again, what time do I get home for breakfast?

2.2

Expressions and statements

An expression is a combination of values, variables, and operators. A value all by itself is considered an expression, and so is a variable, so the following are all legal expressions (assuming that the variable x has been assigned a value):

17
x
x + 17

A statement is a unit of code that the Python interpreter can execute. We have seen two kinds of statement: print and assignment.

Technically an expression is also a statement, but it is probably simpler to think of them as different things. The important difference is that an expression has a value; a statement does not.

Boolean expressions

A boolean expression is an expression that is either true or false. The following examples use the operator ==, which compares two operands and produces True if they are equal and False otherwise:

>>> 5 == 5
True
>>> 5 == 6
False
`

True and False are special values that belong to the type bool; they are not strings:

>>> type(True)
<type 'bool'>
>>> type(False)
<type 'bool'>

The == operator is one of the relational operators; the others are:

  x != y               # x is not equal to y
  x > y                # x is greater than y
  x < y                # x is less than y
  x >= y               # x is greater than or equal to y
  x <= y               # x is less than or equal to y

Although these operations are probably familiar to you, the Python symbols are different from the mathematical symbols. A common error is to use a single equal sign (=) instead of a double equal sign (==). Remember that = is an assignment operator and == is a relational operator. There is no such thing as =< or =>.

Logical operators

There are three logical operators: and, or, and not. The semantics (meaning) of these operators is similar to their meaning in English. For example, x > 0 and x < 10 is true only if x is greater than 0 and less than 10.

n * 2 == 4 or n * 10 == 100 is true if either of the conditions is true, that is, if the number is 2 or 10.

The or expression is true whenever one of the operands is true and the and expression is false whenever one of the operands is false.

Finally, the not operator negates a boolean expression, so not (x > y) is true if x > y is false, that is, if x is less than or equal to y.

Strictly speaking, the operands of the logical operators should be boolean expressions, but Python is not very strict. Any nonzero number is interpreted as “true.”

>>> 17 and True
True

This flexibility can be useful, but there are some subtleties to it that might be confusing. You might want to avoid it (unless you know what you are doing).

2.3

Conditional execution

In order to write useful programs, we almost always need the ability to check conditions and change the behavior of the program accordingly. Conditional statements give us this ability. The simplest form is the if statement:

if x > 0:
    print('x is positive')

The boolean expression after if is called the condition. If it is true, then the indented statement gets executed. If not, nothing happens. if statements have the same structure as function definitions: a header followed by an indented body. Statements like this are called compound statements.

There is no limit on the number of statements that can appear in the body, but there has to be at least one. Occasionally, it is useful to have a body with no statements (usually as a place keeper for code you haven’t written yet). In that case, you can use the pass statement, which does nothing.

if x < 0:
    pass          # need to handle negative values!
#Alternative execution

A second form of the if statement is alternative execution, in which there are two possibilities and the condition determines which one gets executed. The syntax looks like this:

if x%2 == 0:
    print('x is even')
else:
    print('x is odd')

If the remainder when x is divided by 2 is 0, then we know that x is even, and the program displays a message to that effect. If the condition is false, the second set of statements is executed. Since the condition must be true or false, exactly one of the alternatives will be executed. The alternatives are called branches, because they are branches in the flow of execution.

Chained conditionals

Sometimes there are more than two possibilities and we need more than two branches. One way to express a computation like that is a chained conditional:

if x < y:
    print('x is less than y')
elif x > y:
    print('x is greater than y')
else:
    print('x and y are equal')

elif is an abbreviation of “else if.” Again, exactly one branch will be executed. There is no limit on the number of elif statements. If there is an else clause, it has to be at the end, but there doesn’t have to be one.

if choice == 'a':
    draw_a()
elif choice == 'b':
    draw_b()
elif choice == 'c':
    draw_c()

Each condition is checked in order. If the first is false, the next is checked, and so on. If one of them is true, the corresponding branch executes, and the statement ends. Even if more than one condition is true, only the first true branch executes.

Nested conditionals

One conditional can also be nested within another. We could have written the trichotomy example like this:

if x == y:
    print('x and y are equal')
else:
    if x < y:
        print('x is less than y')
    else:
        print('x is greater than y')

The outer conditional contains two branches. The first branch contains a simple statement. The second branch contains another if statement, which has two branches of its own. Those two branches are both simple statements, although they could have been conditional statements as well. Although the indentation of the statements makes the structure apparent, nested conditionals become difficult to read very quickly. In general, it is a good idea to avoid them when you can.

Logical operators often provide a way to simplify nested conditional statements. For example, we can rewrite the following code using a single conditional:

if 0 < x:
    if x < 10:
        print('x is a positive single-digit number.')

The print(statement is executed only if we make it past both conditionals, so we can get the same effect with the and operator:)

if 0 < x and x < 10:
    print('x is a positive single-digit number.')

2.4

A list is a sequence

Like a string, a list is a sequence of values. In a string, the values are characters; in a list, they can be any type. The values in a list are called elements or sometimes items.

There are several ways to create a new list; the simplest is to enclose the elements in square brackets ([ and ]):

[10, 20, 30, 40]
['crunchy frog', 'ram bladder', 'lark vomit']

The first example is a list of four integers. The second is a list of three strings. The elements of a list don’t have to be the same type. The following list contains a string, a float, an integer, and (lo!) another list:

['spam', 2.0, 5, [10, 20]]

A list within another list is nested. A list that contains no elements is called an empty list; you can create one with empty brackets, [].

As you might expect, you can assign list values to variables:

>>> cheeses = ['Cheddar', 'Edam', 'Gouda']
>>> numbers = [17, 123]
>>> empty = []
>>> print(cheeses, numbers, empty)
['Cheddar', 'Edam', 'Gouda'] [17, 123] []

Lists are mutable

The syntax for accessing the elements of a list is the same as for accessing the characters of a string—the bracket operator. The expression inside the brackets specifies the index. Remember that the indices start at 0:

>>> print(cheeses[0])
Cheddar

Unlike strings, lists are mutable. When the bracket operator appears on the left side of an assignment, it identifies the element of the list that will be assigned.

>>> numbers = [17, 123]
>>> numbers[1] = 5
>>> print(numbers)
[17, 5]

The one-eth element of numbers, which used to be 123, is now 5. You can think of a list as a relationship between indices and elements. This relationship is called a mapping; each index “maps to” one of the elements. Figure 10.1 shows the state diagram for cheeses, numbers and empty: 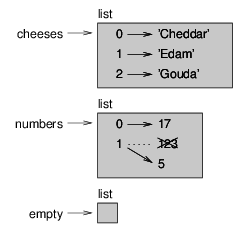Figure 10.1: State diagram.

Lists are represented by boxes with the word “list” outside and the elements of the list inside. cheeses refers to a list with three elements indexed 0, 1 and 2. numbers contains two elements; the diagram shows that the value of the second element has been reassigned from 123 to 5. empty refers to a list with no elements.

List indices work the same way as string indices:

Any integer expression can be used as an index. If you try to read or write an element that does not exist, you get an IndexError. If an index has a negative value, it counts backward from the end of the list.

2.5

List operations

The + operator concatenates lists:

>>> a = [1, 2, 3]
>>> b = [4, 5, 6]
>>> c = a + b
>>> print(c)
[1, 2, 3, 4, 5, 6]

Similarly, the * operator repeats a list a given number of times:

>>> [0] * 4
[0, 0, 0, 0]
>>> [1, 2, 3] * 3
[1, 2, 3, 1, 2, 3, 1, 2, 3]

The first example repeats [0] four times. The second example repeats the list [1, 2, 3] three times. 10.5 List slices

The slice operator works on lists:

>>> t = ['a', 'b', 'c', 'd', 'e', 'f']
>>> t[1:3]
['b', 'c']
>>> t[:4]
['a', 'b', 'c', 'd']
>>> t[3:]
['d', 'e', 'f']

If you omit the first index, the slice starts at the beginning. If you omit the second, the slice goes to the end. So if you omit both, the slice is a copy of the whole list.

>>> t[:]
['a', 'b', 'c', 'd', 'e', 'f']

Since lists are mutable, it is often useful to make a copy before performing operations that fold, spindle or mutilate lists. A slice operator on the left side of an assignment can update multiple elements:

>>> t = ['a', 'b', 'c', 'd', 'e', 'f']
>>> t[1:3] = ['x', 'y']
>>> print(t)
['a', 'x', 'y', 'd', 'e', 'f']

List methods

Python provides methods that operate on lists. For example, append adds a new element to the end of a list:

>>> t = ['a', 'b', 'c']
>>> t.append('d')
>>> print(t)
['a', 'b', 'c', 'd']

Deleting elements

There are several ways to delete elements from a list. If you know the index of the element you want, you can use pop:

>>> t = ['a', 'b', 'c']
>>> x = t.pop(1)
>>> print(t)
['a', 'c']
>>> print(x)
b

pop modifies the list and returns the element that was removed. If you don’t provide an index, it deletes and returns the last element.

If you know the element you want to remove you can use remove:

>>> t = ['a', 'b', 'c']
>>> t.remove('b')
>>> print(t)
['a', 'c']

2.6

The in operator works on lists.

>>> cheeses = ['Cheddar', 'Edam', 'Gouda']
>>> 'Edam' in cheeses
True
>>> 'Brie' in cheeses
False

2.7

The while statement

Computers are often used to automate repetitive tasks. Repeating identical or similar tasks without making errors is something that computers do well and people do poorly.

Here is an example countdown snippet that uses a while statement:

while n > 0:
    print(n)
    n = n-1
print('Blastoff!')

You can almost read the while statement as if it were English. It means, “While n is greater than 0, display the value of n and then reduce the value of n by 1. When you get to 0, display the word Blastoff!” More formally, here is the flow of execution for a while statement:

1. Evaluate the condition, yielding True or False.
2. If the condition is false, exit the while statement and continue execution at the next statement.
3. If the condition is true, execute the body and then go back to step 1.

This type of flow is called a loop because the third step loops back around to the top.

The body of the loop should change the value of one or more variables so that eventually the condition becomes false and the loop terminates. Otherwise the loop will repeat forever, which is called an infinite loop. An endless source of amusement for computer scientists is the observation that the directions on shampoo, “Lather, rinse, repeat,” are an infinite loop.

In the case of countdown, we can prove that the loop terminates because we know that the value of n is finite, and we can see that the value of n gets smaller each time through the loop, so eventually we have to get to 0. In other cases, it is not so easy to tell:

while n != 1:
    print n,
    if n%2 == 0:        # n is even
        n = n/2
    else:               # n is odd
        n = n*3+1

The condition for this loop is n != 1, so the loop will continue until n is 1, which makes the condition false. Each time through the loop, the program outputs the value of n and then checks whether it is even or odd. If it is even, n is divided by 2. If it is odd, the value of n is replaced with n*3+1. For example, if the argument passed to sequence is 3, the resulting sequence is 3, 10, 5, 16, 8, 4, 2, 1.

Since n sometimes increases and sometimes decreases, there is no obvious proof that n will ever reach 1, or that the program terminates. For some particular values of n, we can prove termination. For example, if the starting value is a power of two, then the value of n will be even each time through the loop until it reaches 1. The previous example ends with such a sequence, starting with 16.

The hard question is whether we can prove that this program terminates for all positive values of n. So far, no one has been able to prove it or disprove it! (See http://en.wikipedia.org/wiki/Collatz_conjecture.)

Unit 3

3.1

Function calls

In the context of programming, a function is a named sequence of statements that performs a computation. When you define a function, you specify the name and the sequence of statements. Later, you can “call” the function by name. We have already seen one example of a function call:

>>> type(32)
<type 'int'>

The name of the function is type. The expression in parentheses is called the argument of the function. The result, for this function, is the type of the argument. It is common to say that a function “takes” an argument and “returns” a result. The result is called the return value.

Type conversion functions

Python provides built-in functions that convert values from one type to another. The int function takes any value and converts it to an integer, if it can, or complains otherwise:

>>> int('32')
32
>>> int('Hello')
ValueError: invalid literal for int(): Hello

int can convert floating-point values to integers, but it doesn’t round off; it chops off the fraction part:

>>> int(3.99999)
3
>>> int(-2.3)
-2
float converts integers and strings to floating-point numbers:
>>> float(32)
32.0
>>> float('3.14159')
3.14159
Finally, str converts its argument to a string:
>>> str(32)
'32'
>>> str(3.14159)
'3.14159'

Math functions

Python has a math module that provides most of the familiar mathematical functions. A module is a file that contains a collection of related functions.

Before we can use the module, we have to import it:

>>> import math
This statement creates a module object named math. If you print the module object, you get some information about it:
>>> print(math)
<module 'math' (built-in)>

The module object contains the functions and variables defined in the module. To access one of the functions, you have to specify the name of the module and the name of the function, separated by a dot (also known as a period). This format is called dot notation.

>>> ratio = signal_power / noise_power
>>> decibels = 10 * math.log10(ratio)

>>> radians = 0.7
>>> height = math.sin(radians)
`

The first example uses log10 to compute a signal-to-noise ratio in decibels (assuming that signal_power and noise_power are defined). The math module also provides log, which computes logarithms base e. The second example finds the sine of radians. The name of the variable is a hint that sin and the other trigonometric functions (cos, tan, etc.) take arguments in radians. To convert from degrees to radians, divide by 360 and multiply by 2 π:

>>> degrees = 45
>>> radians = degrees / 360.0 * 2 * math.pi
>>> math.sin(radians)
0.707106781187

The expression math.pi gets the variable pi from the math module. The value of this variable is an approximation of π, accurate to about 15 digits. If you know your trigonometry, you can check the previous result by comparing it to the square root of two divided by two:

>>> math.sqrt(2) / 2.0
0.707106781187

Composition

So far, we have looked at the elements of a program—variables, expressions, and statements—in isolation, without talking about how to combine them.

One of the most useful features of programming languages is their ability to take small building blocks and compose them. For example, the argument of a function can be any kind of expression, including arithmetic operators:

x = math.sin(degrees / 360.0 * 2 * math.pi)
And even function calls:
x = math.exp(math.log(x+1))

Almost anywhere you can put a value, you can put an arbitrary expression, with one exception: the left side of an assignment statement has to be a variable name. Any other expression on the left side is a syntax error (we will see exceptions to this rule later).

>>> minutes = hours * 60                 # right
>>> hours * 60 = minutes                 # wrong!
SyntaxError: can't assign to operator

3.2

Adding new functions

So far, we have only been using the functions that come with Python, but it is also possible to add new functions. A function definition specifies the name of a new function and the sequence of statements that execute when the function is called. Here is an example:

def print_lyrics():
    print("I'm a lumberjack, and I'm okay.")
    print("I sleep all night and I work all day.")

def is a keyword that indicates that this is a function definition. The name of the function is print_lyrics. The rules for function names are the same as for variable names: letters, numbers and some punctuation marks are legal, but the first character can’t be a number. You can’t use a keyword as the name of a function, and you should avoid having a variable and a function with the same name. The empty parentheses after the name indicate that this function doesn’t take any arguments.

The first line of the function definition is called the header; the rest is called the body. The header has to end with a colon and the body has to be indented. By convention, the indentation is always four spaces. The body can contain any number of statements.

The strings in the print statements are enclosed in double quotes. Single quotes and double quotes do the same thing; most people use single quotes except in cases like this where a single quote (which is also an apostrophe) appears in the string.

If you type a function definition in interactive mode, the interpreter prints ellipses (...) to let you know that the definition isn’t complete:

>>> def print_lyrics():
...     print("I'm a lumberjack, and I'm okay.")
...     print("I sleep all night and I work all day.")
...

To end the function, you have to enter an empty line (this is not necessary in a script). Defining a function creates a variable with the same name.

>>> print(print_lyrics)
<function print_lyrics at 0xb7e99e9c>
>>> type(print_lyrics)
<type 'function'>

The value of print_lyrics is a function object, which has type 'function'. The syntax for calling the new function is the same as for built-in functions:

>>> print_lyrics()
I'm a lumberjack, and I'm okay.
I sleep all night and I work all day.
Once you have defined a function, you can use it inside another function. For example, to repeat the previous refrain, we could write a function called repeat_lyrics:
def repeat_lyrics():
    print_lyrics()
    print_lyrics()
And then call repeat_lyrics:
>>> repeat_lyrics()
I'm a lumberjack, and I'm okay.
I sleep all night and I work all day.
I'm a lumberjack, and I'm okay.
I sleep all night and I work all day.
But that’s not really how the song goes.

Definitions and uses

Pulling together the code fragments from the previous section, the whole program looks like this:

def print_lyrics():
    print("I'm a lumberjack, and I'm okay.")
    print("I sleep all night and I work all day.")

def repeat_lyrics():
    print_lyrics()
    print_lyrics()

repeat_lyrics()

This program contains two function definitions: print_lyrics and repeat_lyrics. Function definitions get executed just like other statements, but the effect is to create function objects. The statements inside the function do not get executed until the function is called, and the function definition generates no output. As you might expect, you have to create a function before you can execute it. In other words, the function definition has to be executed before the first time it is called.

Exercise 1

Move the last line of this program to the top, so the function call appears before the definitions. Run the program and see what error message you get.

Exercise 2

Move the function call back to the bottom and move the definition of print_lyrics after the definition of repeat_lyrics. What happens when you run this program?

Flow of execution

In order to ensure that a function is defined before its first use, you have to know the order in which statements are executed, which is called the flow of execution.

Execution always begins at the first statement of the program. Statements are executed one at a time, in order from top to bottom.

Function definitions do not alter the flow of execution of the program, but remember that statements inside the function are not executed until the function is called.

A function call is like a detour in the flow of execution. Instead of going to the next statement, the flow jumps to the body of the function, executes all the statements there, and then comes back to pick up where it left off.

That sounds simple enough, until you remember that one function can call another. While in the middle of one function, the program might have to execute the statements in another function. But while executing that new function, the program might have to execute yet another function!

Fortunately, Python is good at keeping track of where it is, so each time a function completes, the program picks up where it left off in the function that called it. When it gets to the end of the program, it terminates.

What’s the moral of this sordid tale? When you read a program, you don’t always want to read from top to bottom. Sometimes it makes more sense if you follow the flow of execution.

Parameters and arguments

Some of the built-in functions we have seen require arguments. For example, when you call math.sin you pass a number as an argument. Some functions take more than one argument: math.pow takes two, the base and the exponent.

Inside the function, the arguments are assigned to variables called parameters. Here is an example of a user-defined function that takes an argument:

def print_twice(bruce):
    print(bruce)
    print(bruce)

This function assigns the argument to a parameter named bruce. When the function is called, it prints the value of the parameter (whatever it is) twice. This function works with any value that can be printed.

>>> print_twice('Spam')
Spam
Spam
>>> print_twice(17)
17
17
>>> print_twice(math.pi)
3.14159265359
3.14159265359

The same rules of composition that apply to built-in functions also apply to user-defined functions, so we can use any kind of expression as an argument for print_twice:

>>> print_twice('Spam '*4)
Spam Spam Spam Spam
Spam Spam Spam Spam
>>> print_twice(math.cos(math.pi))
-1.0
-1.0

The argument is evaluated before the function is called, so in the examples the expressions 'Spam '*4 and math.cos(math.pi) are only evaluated once. You can also use a variable as an argument:

>>> michael = 'Eric, the half a bee.'
>>> print_twice(michael)
Eric, the half a bee.
Eric, the half a bee.

The name of the variable we pass as an argument (michael) has nothing to do with the name of the parameter (bruce). It doesn’t matter what the value was called back home (in the caller); here in print_twice, we call everybody bruce.

3.3

Return values

Some of the built-in functions we have used, such as the math functions, produce results. Calling the function generates a value, which we usually assign to a variable or use as part of an expression.

e = math.exp(1.0)
height = radius * math.sin(radians)

All of the functions we have written so far are void; they print something or move turtles around, but their return value is None. In this chapter, we are (finally) going to write fruitful functions. The first example is area, which returns the area of a circle with the given radius:

def area(radius):
    temp = math.pi * radius**2
    return temp

This statement means: “Return immediately from this function and use the following expression as a return value.” The expression can be arbitrarily complicated, so we could have written this function more concisely:

def area(radius):
    return math.pi * radius**2

On the other hand, temporary variables like temp often make debugging easier. Sometimes it is useful to have multiple return statements, one in each branch of a conditional:

def absolute_value(x):
    if x < 0:
        return -x
    else:
        return x

Since these return statements are in an alternative conditional, only one will be executed. As soon as a return statement executes, the function terminates without executing any subsequent statements. Code that appears after a return statement, or any other place the flow of execution can never reach, is called dead code.

It is a good idea to ensure that every possible path through the program hits a return statement. For example:

def absolute_value(x):
    if x < 0:
        return -x
    if x > 0:
        return x

This function is incorrect because if x happens to be 0, neither condition is true, and the function ends without hitting a return statement. If the flow of execution gets to the end of a function, the return value is None, which is not the absolute value of 0.

>>> print(absolute_value(0))
None

By the way, Python provides a built-in function called abs that computes absolute values.

Exercise 1

Write a compare function that returns 1 if x > y, 0 if x == y, and -1 if x < y.

3.4

Variables and parameters are local

When you create a variable inside a function, it is local, which means that it only exists inside the function. For example:

def cat_twice(part1, part2):
    cat = part1 + part2
    print_twice(cat)

This function takes two arguments, concatenates them, and prints the result twice. Here is an example that uses it:

>>> line1 = 'Bing tiddle '
>>> line2 = 'tiddle bang.'
>>> cat_twice(line1, line2)
Bing tiddle tiddle bang.
Bing tiddle tiddle bang.

When cat_twice terminates, the variable cat is destroyed. If we try to print(it, we get an exception:)

>>> print(cat)
NameError: name 'cat' is not defined

Parameters are also local. For example, outside print_twice, there is no such thing as bruce.

Stack diagrams

To keep track of which variables can be used where, it is sometimes useful to draw a stack diagram. Like state diagrams, stack diagrams show the value of each variable, but they also show the function to which each variable belongs.

Each function is represented by a frame. A frame is a box with the name of a function beside it and the parameters and variables of the function inside it. The stack diagram for the previous example looks like this:

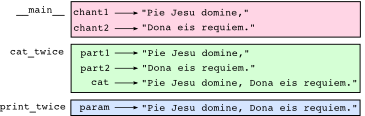
Stack diagram The order of the stack shows the flow of execution. printtwice was called by cattwice, and cattwice was called by _main, which is a special name for the topmost function. When you create a variable outside of any function, it belongs to __main.

Each parameter refers to the same value as its corresponding argument. So, part1 has the same value as chant1, part2 has the same value as chant2, and param has the same value as cat.

If an error occurs during a function call, Python prints the name of the function, and the name of the function that called it, and the name of the function that called that, all the way back to the top most function.

To see how this works, create a Python script named tryme2.py that looks like this:

def print_twice(param):
    print(param)
    print(param)
    print(cat)

def cat_twice(part1, part2):
    cat = part1 + part2
    print_twice(cat)

chant1 = "Pie Jesu domine, "
chant2 = "Dona eis requim."
cat_twice(chant1, chant2)

We’ve added the statement, print(cat) inside the print_twice function, but cat is not defined there. Running this script will produce an error message like this:

Traceback (innermost last):
  File "tryme2.py", line 12, in <module>
    cat_twice(chant1, chant2)
  File "tryme2.py", line 8, in cat_twice
    print_twice(cat)
  File "tryme2.py", line 4, in print_twice
    print(cat)
NameError: global name 'cat' is not defined

This list of functions is called a traceback. It tells you what program file the error occurred in, and what line, and what functions were executing at the time. It also shows the line of code that caused the error.

Notice the similarity between the traceback and the stack diagram. It’s not a coincidence. In fact, another common name for a traceback is a stack trace.

Aliasing

If a refers to an object and you assign b = a, then both variables refer to the same object:

>>> a = [1, 2, 3]
>>> b = a
>>> b is a
True

The state diagram looks like:

The association of a variable with an object is called a reference. In this example, there are two references to the same object. An object with more than one reference has more than one name, so we say that the object is aliased.

If the aliased object is mutable, changes made with one alias affect the other:

>>> b[0] = 17
>>> print(a)
[17, 2, 3]

Although this behavior can be useful, it is error-prone. In general, it is safer to avoid aliasing when you are working with mutable objects.

List arguments

When you pass a list to a function, the function gets a reference to the list. If the function modifies a list parameter, the caller sees the change. For example, delete_head removes the first element from a list:

def delete_head(t):
    del t[0]
Here’s how it is used:
>>> letters = ['a', 'b', 'c']
>>> delete_head(letters)
>>> print(letters)
['b', 'c']

The parameter t and the variable letters are aliases for the same object. The stack diagram looks like the following:

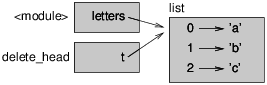
Since the list is shared by two frames, I drew it between them. It is important to distinguish between operations that modify lists and operations that create new lists. For example, the append method modifies a list, but the + operator creates a new list:

>>> t1 = [1, 2]
>>> t2 = t1.append(3)
>>> print(t1)
[1, 2, 3]
>>> print(t2)
None

>>> t3 = t1 + [4]
>>> print(t3)
[1, 2, 3, 4]

This difference is important when you write functions that are supposed to modify lists. For example, this function does not delete the head of a list:

def bad_delete_head(t):
    t = t[1:]              # WRONG!

The slice operator creates a new list and the assignment makes t refer to it, but none of that has any effect on the list that was passed as an argument. An alternative is to write a function that creates and returns a new list. For example, tail returns all but the first element of a list:

def tail(t):
    return t[1:]
This function leaves the original list unmodified. Here’s how it is used:
>>> letters = ['a', 'b', 'c']
>>> rest = tail(letters)
>>> print(rest)
['b', 'c']

Unit 4

4.1 Traversing a list

The most common way to traverse the elements of a list is with a for loop. The syntax is the same as for strings:

for cheese in cheeses:
    print(cheese)

This works well if you only need to read the elements of the list. A for loop over an empty list never executes the body:

for x in []: print('This never happens.')

Although a list can contain another list, the nested list still counts as a single element. The length of this list is four: ['spam', 1, ['Brie', 'Roquefort', 'Pol le Veq'], [1, 2, 3]]

Traversing a String

A lot of computations involve processing a string one character at a time. Often they start at the beginning, select each character in turn, do something to it, and continue until the end. This pattern of processing is called a traversal. One way to write a traversal is with a while loop:

index = 0
while index < len(fruit):
    letter = fruit[index]
    print(letter)
    index = index + 1

This loop traverses the string and displays each letter on a line by itself. The loop condition is index < len(fruit), so when index is equal to the length of the string, the condition is false, and the body of the loop is not executed. The last character accessed is the one with the index len(fruit)-1, which is the last character in the string.

Exercise 1

Write a function that takes a string as an argument and displays the letters backward, one per line.

Another way to write a traversal is with a for loop:

for char in fruit:
    print(char)

Each time through the loop, the next character in the string is assigned to the variable char. The loop continues until no characters are left.

The following example shows how to use concatenation (string addition) and a for loop to generate an abecedarian series (that is, in alphabetical order). In Robert McCloskey’s book Make Way for Ducklings, the names of the ducklings are Jack, Kack, Lack, Mack, Nack, Ouack, Pack, and Quack. This loop outputs these names in order:

prefixes = 'JKLMNOPQ'
suffix = 'ack'

for letter in prefixes:
    print(letter + suffix)
The output is:
Jack
Kack
Lack
Mack
Nack
Oack
Pack
Qack

Of course, that’s not quite right because “Ouack” and “Quack” are misspelled.

Exercise 2

Modify the program to fix this error.

Looping and counting

The following program counts the number of times the letter a appears in a string:

word = 'banana'
count = 0
for letter in word:
    if letter == 'a':
        count = count + 1
print(count)

This program demonstrates another pattern of computation called a counter. The variable count is initialized to 0 and then incremented each time an a is found. When the loop exits, count contains the result—the total number of a’s.

Exercise 5

Encapsulate this code in a function named count, and generalize it so that it accepts the string and the letter as arguments.

Exercise 6

Rewrite this function so that instead of traversing the string, it uses the three-parameter version of find from the previous section.

4.2

For Loop Using Range

As mentioned, the most common way to traverse the elements of a list is with a for loop. If you want to write or update the elements, you need the indices. A common way to do that is to combine the functions range and len:

for i in range(len(numbers)):
    numbers[i] = numbers[i] * 2

This loop traverses the list and updates each element. len returns the number of elements in the list. range returns a list of indices from 0 to n−1, where n is the length of the list. Each time through the loop i gets the index of the next element. The assignment statement in the body uses i to read the old value of the element and to assign the new value.

Debugging

When you use indices to traverse the values in a sequence, it is tricky to get the beginning and end of the traversal right. Here is a function that is supposed to compare two words and return True if one of the words is the reverse of the other, but it contains two errors:

def is_reverse(word1, word2):
    if len(word1) != len(word2):
        return False

    i = 0
    j = len(word2)

    while j > 0:
        if word1[i] != word2[j]:
            return False
        i = i+1
        j = j-1

    return True

The first if statement checks whether the words are the same length. If not, we can return False immediately and then, for the rest of the function, we can assume that the words are the same length. This is an example of the guardian pattern in Section 6.8. i and j are indices: i traverses word1 forward while j traverses word2 backward. If we find two letters that don’t match, we can return False immediately. If we get through the whole loop and all the letters match, we return True.

If we test this function with the words “pots” and “stop”, we expect the return value True, but we get an IndexError:

>>> is_reverse('pots', 'stop')
...
  File "reverse.py", line 15, in is_reverse
    if word1[i] != word2[j]:
IndexError: string index out of range

For debugging this kind of error, my first move is to print the values of the indices immediately before the line where the error appears.

    while j > 0:
        print (i, j)        # print here

        if word1[i] != word2[j]:
            return False
        i = i+1
        j = j-1

Now when I run the program again, I get more information:

>>> is_reverse('pots', 'stop')
0 4
...
IndexError: string index out of range

The first time through the loop, the value of j is 4, which is out of range for the string 'pots'. The index of the last character is 3, so the initial value for j should be len(word2)-1. If I fix that error and run the program again, I get:

>>> is_reverse('pots', 'stop')
0 3
1 2
2 1
True

This time we get the right answer, but it looks like the loop only ran three times, which is suspicious. To get a better idea of what is happening, it is useful to draw a state diagram. During the first iteration, the frame for is_reverse is shows in Figure 1.

Figure 1: State diagram.

I took a little license by arranging the variables in the frame and adding dotted lines to show that the values of i and j indicate characters in word1 and word2.

Exercise

Starting with this diagram, execute the program on paper, changing the values of i and j during each iteration. Find and fix the second error in this function.

Unit 5

5.1

Dictionaries

A dictionary is like a list, but more general. In a list, the indices have to be integers; in a dictionary they can be (almost) any type. You can think of a dictionary as a mapping between a set of indices (which are called keys) and a set of values. Each key maps to a value. The association of a key and a value is called a key-value pair or sometimes an item.

As an example, we’ll build a dictionary that maps from English to Spanish words, so the keys and the values are all strings.

The function dict creates a new dictionary with no items. Because dict is the name of a built-in function, you should avoid using it as a variable name.

>>> eng2sp = dict()
>>> print(eng2sp)
{}

The squiggly-brackets, {}, represent an empty dictionary.

You can create a new dictionary with three items:

>>> eng2sp = {'one': 'uno', 'two': 'dos', 'three': 'tres'}

But if you print eng2sp, you might be surprised:

>>> print(eng2sp)
{'one': 'uno', 'three': 'tres', 'two': 'dos'}

The order of the key-value pairs is not the same. In fact, if you type the same example on your computer, you might get a different result. In general, the order of items in a dictionary is unpredictable. But that’s not a problem because the elements of a dictionary are never indexed with integer indices. Instead, you use the keys to look up the corresponding values:

>>> print eng2sp['two']
'dos'

The key ’two’ always maps to the value 'dos' so the order of the items doesn’t matter. If the key isn’t in the dictionary, you get an exception:

>>> print eng2sp['four']
KeyError: 'four'

Dictionaries have a method called get that takes a key and a default value. If the key appears in the dictionary, get returns the corresponding value; otherwise it returns the default value. For example:

>>> h = histogram('a')
>>> print h
{'a': 1}
>>> h.get('a', 0)
1
>>> h.get('b', 0)
0

The `len`` function works on dictionaries; it returns the number of key-value pairs:

>>> len(eng2sp)
3

The in operator works on dictionaries; it tells you whether something appears as a key in the dictionary (appearing as a value is not good enough).

>>> 'one' in eng2sp
True
>>> 'uno' in eng2sp
False

5.2

To add items to the dictionary, you can use square brackets:

>>> eng2sp = {}
>>> print(eng2sp)
{}
>>> eng2sp['one'] = 'uno'

This line creates an item that maps from the key ’one’ to the value 'uno'. If we print the dictionary again, we see a key-value pair with a colon between the key and value:

>>> print(eng2sp)
{'one': 'uno'}

Dictionary as a set of counters

Suppose you are given a string and you want to count how many times each letter appears. There are several ways you could do it:

You could create 26 variables, one for each letter of the alphabet. Then you could traverse the string and, for each character, increment the corresponding counter, probably using a chained conditional.

You could create a list with 26 elements. Then you could convert each character to a number (using the built-in function ord), use the number as an index into the list, and increment the appropriate counter.

You could create a dictionary with characters as keys and counters as the corresponding values. The first time you see a character, you would add an item to the dictionary. After that you would increment the value of an existing item.

Each of these options performs the same computation, but each of them implements that computation in a different way.

An implementation is a way of performing a computation; some implementations are better than others. For example, an advantage of the dictionary implementation is that we don’t have to know ahead of time which letters appear in the string and we only have to make room for the letters that do appear.

Here is what the code might look like:

def histogram(s):
    d = dict()
    for c in s:
        if c not in d:
            d[c] = 1
        else:
            d[c] += 1
    return d

The name of the function is histogram, which is a statistical term for a set of counters (or frequencies). The first line of the function creates an empty dictionary. The for loop traverses the string. Each time through the loop, if the character c is not in the dictionary, we create a new item with key c and the initial value 1 (since we have seen this letter once). If c is already in the dictionary we increment d[c].

Here’s how it works:

>>> h = histogram('brontosaurus')
>>> print h
{'a': 1, 'b': 1, 'o': 2, 'n': 1, 's': 2, 'r': 2, 'u': 2, 't': 1}

The histogram indicates that the letters ’a’ and 'b' appear once; 'o' appears twice, and so on.

5.3

Dictionaries and lists

Lists can appear as values in a dictionary. For example, if you were given a dictionary that maps from letters to frequencies, you might want to invert it; that is, create a dictionary that maps from frequencies to letters. Since there might be several letters with the same frequency, each value in the inverted dictionary should be a list of letters.

Here is a function that inverts a dictionary:

def invert_dict(d):
    inverse = dict()
    for key in d:
        val = d[key]
        if val not in inverse:
            inverse[val] = [key]
        else:
            inverse[val].append(key)
    return inverse

Each time through the loop, key gets a key from d and val gets the corresponding value. If val is not in inverse, that means we haven’t seen it before, so we create a new item and initialize it with a singleton (a list that contains a single element). Otherwise we have seen this value before, so we append the corresponding key to the list. Here is an example:

>>> hist = histogram('parrot')
>>> print hist
{'a': 1, 'p': 1, 'r': 2, 't': 1, 'o': 1}
>>> inverse = invert_dict(hist)
>>> print inverse
{1: ['a', 'p', 't', 'o'], 2: ['r']}

Lists can be values in a dictionary, as this example shows, but they cannot be keys. Here’s what happens if you try:

>>> t = [1, 2, 3]
>>> d = dict()
>>> d[t] = 'oops'
Traceback (most recent call last):
  File "<stdin>", line 1, in ?
TypeError: list objects are unhashable

A dictionary is implemented using a hashtable and that means that the keys have to be hashable. A hash is a function that takes a value (of any kind) and returns an integer. Dictionaries use these integers, called hash values, to store and look up key-value pairs.

This system works fine if the keys are immutable. But if the keys are mutable, like lists, bad things happen. For example, when you create a key-value pair, Python hashes the key and stores it in the corresponding location. If you modify the key and then hash it again, it would go to a different location. In that case you might have two entries for the same key, or you might not be able to find a key. Either way, the dictionary wouldn’t work correctly.

That’s why the keys have to be hashable, and why mutable types like lists aren’t.

Since lists and dictionaries are mutable, they can’t be used as keys, but they can be used as values.

5.4

Looping and dictionaries

If you use a dictionary in a for statement, it traverses the keys of the dictionary. For example, print_hist prints each key and the corresponding value:

def print_hist(h):
    for c in h:
        print c, h[c]

Here’s what the output looks like:

>>> h = histogram('parrot')
>>> print_hist(h)
a 1
p 1
r 2
t 1
o 1

Again, the keys are in no particular order.

Dictionaries have a method called keys that returns the keys of the dictionary, in no particular order, as a list.

Unit 6

6.1

User-defined types

We have used many of Python’s built-in types; now we are going to define a new type. As an example, we will create a type called Point that represents a point in two-dimensional space.

In mathematical notation, points are often written in parentheses with a comma separating the coordinates. For example, (0,0) represents the origin, and (x,y) represents the point x units to the right and y units up from the origin.

There are several ways we might represent points in Python:

We could store the coordinates separately in two variables, x and y. We could store the coordinates as elements in a list or tuple. We could create a new type to represent points as objects. Creating a new type is (a little) more complicated than the other options, but it has advantages that will be apparent soon.

A user-defined type is also called a class. A class definition looks like this:

class Point(object):
    """Represents a point in 2-D space."""

This header indicates that the new class is a Point, which is a kind of object, which is a built-in type. The body is a docstring that explains what the class is for. You can define variables and functions inside a class definition, but we will get back to that later.

Defining a class named Point creates a class object.

>>> print Point
<class '__main__.Point'>

Because Point is defined at the top level, its “full name” is main.Point. The class object is like a factory for creating objects. To create a Point, you call Point as if it were a function.

>>> blank = Point()
>>> print blank
<__main__.Point instance at 0xb7e9d3ac>

The return value is a reference to a Point object, which we assign to blank. Creating a new object is called instantiation, and the object is an instance of the class. When you print an instance, Python tells you what class it belongs to and where it is stored in memory (the prefix 0x means that the following number is in hexadecimal).

Attributes

You can assign values to an instance using dot notation:

>>> blank.x = 3.0
>>> blank.y = 4.0

This syntax is similar to the syntax for selecting a variable from a module, such as math.pi or string.whitespace. In this case, though, we are assigning values to named elements of an object. These elements are called attributes. As a noun, “AT-trib-ute” is pronounced with emphasis on the first syllable, as opposed to “a-TRIB-ute,” which is a verb.

You can read the value of an attribute using the same syntax:

>>> print blank.y
4.0
>>> x = blank.x
>>> print x
3.0

The expression blank.x means, “Go to the object blank refers to and get the value of x.” In this case, we assign that value to a variable named x. There is no conflict between the variable x and the attribute x. You can use dot notation as part of any expression. For example:

>>> print '(%g, %g)' % (blank.x, blank.y)
(3.0, 4.0)
>>> distance = math.sqrt(blank.x**2 + blank.y**2)
>>> print distance
5.0

You can pass an instance as an argument in the usual way. For example:

def print_point(p):
    print '(%g, %g)' % (p.x, p.y)

print_point takes a point as an argument and displays it in mathematical notation. To invoke it, you can pass blank as an argument:

>>> print_point(blank)
(3.0, 4.0)

Inside the function, p is an alias for blank, so if the function modifies p, blank changes.

Exercises

Exercise 1 Write a function called distance_between_points that takes two Points as arguments and returns the distance between them.

Rectangles

Sometimes it is obvious what the attributes of an object should be, but other times you have to make decisions. For example, imagine you are designing a class to represent rectangles. What attributes would you use to specify the location and size of a rectangle? You can ignore angle; to keep things simple, assume that the rectangle is either vertical or horizontal.

There are at least two possibilities:

You could specify one corner of the rectangle (or the center), the width, and the height. You could specify two opposing corners. At this point it is hard to say whether either is better than the other, so we’ll implement the first one, just as an example. Here is the class definition:

class Rectangle(object):
    """Represents a rectangle.

    attributes: width, height, corner.
    """

The docstring lists the attributes: width and height are numbers; corner is a Point object that specifies the lower-left corner. To represent a rectangle, you have to instantiate a Rectangle object and assign values to the attributes:

box = Rectangle()
box.width = 100.0
box.height = 200.0
box.corner = Point()
box.corner.x = 0.0
box.corner.y = 0.0

The expression box.corner.x means, “Go to the object box refers to and select the attribute named corner; then go to that object and select the attribute named x.”

Instances as return values

Functions can return instances. For example, find_center takes a Rectangle as an argument and returns a Point that contains the coordinates of the center of the Rectangle:

def find_center(rect):
    p = Point()
    p.x = rect.corner.x + rect.width/2.0
    p.y = rect.corner.y + rect.height/2.0
    return p

Here is an example that passes box as an argument and assigns the resulting Point to center:

>>> center = find_center(box)
>>> print_point(center)
(50.0, 100.0)

Objects are mutable

You can change the state of an object by making an assignment to one of its attributes. For example, to change the size of a rectangle without changing its position, you can modify the values of width and height:

box.width = box.width + 50
box.height = box.width + 100

You can also write functions that modify objects. For example, grow_rectangle takes a Rectangle object and two numbers, dwidth and dheight, and adds the numbers to the width and height of the rectangle:

def grow_rectangle(rect, dwidth, dheight):
    rect.width += dwidth
    rect.height += dheight

Here is an example that demonstrates the effect:

>>> print box.width
100.0
>>> print box.height
200.0
>>> grow_rectangle(box, 50, 100)
>>> print box.width
150.0
>>> print box.height
300.0

Inside the function, rect is an alias for box, so if the function modifies rect, box changes.

Exercises

Exercise 1 Write a function named move_rectangle that takes a Rectangle and two numbers named dx and dy. It should change the location of the rectangle by adding dx to the x coordinate of corner and adding dy to the y coordinate of corner.

6.2

The init method

The init method (short for “initialization”) is a special method that gets invoked when an object is instantiated. Its full name is init (two underscore characters, followed by init, and then two more underscores). An init method for the Time class might look like this:

class Time(object):
    def __init__(self, hour=0, minute=0, second=0):
        self.hour = hour
        self.minute = minute
        self.second = second

It is common for the parameters of init to have the same names as the attributes. The statement

        self.hour = hour

stores the value of the parameter hour as an attribute of self. The parameters are optional, so if you call Time with no arguments, you get the default values.

>>> time = Time()
>>> time.print_time()
00:00:00
If you provide one argument, it overrides hour:
>>> time = Time (9)
>>> time.print_time()
09:00:00
If you provide two arguments, they override hour and minute.
>>> time = Time(9, 45)
>>> time.print_time()
09:45:00

And if you provide three arguments, they override all three default values.

Debugging

It is legal to add attributes to objects at any point in the execution of a program, but if you are a stickler for type theory, it is a dubious practice to have objects of the same type with different attribute sets. It is usually a good idea to initialize all of an object’s attributes in the init method.

If you are not sure whether an object has a particular attribute, you can use the built-in function hasattr (see Section 15.7).

Another way to access the attributes of an object is through the special attribute dict, which is a dictionary that maps attribute names (as strings) and values:

p = Point(3, 4) print p.dict {'y': 4, 'x': 3} For purposes of debugging, you might find it useful to keep this function handy: def printattributes(obj): for attr in obj._dict: print attr, getattr(obj, attr) print_attributes traverses the items in the object’s dictionary and prints each attribute name and its corresponding value. The built-in function getattr takes an object and an attribute name (as a string) and returns the attribute’s value.

6.3

Printing objects

We defined a class named Time and a function print_time:

class Time(object):
    """Represents the time of day."""

def print_time(time):
    print(str(time.hour) + ":" + str(time.minute) + ":" + str(time.second))

To call this function, you have to pass a Time object as an argument:

>>> start = Time()
>>> start.hour = 9
>>> start.minute = 45
>>> start.second = 00
>>> print_time(start)
09:45:00

To make print_time a method, all we have to do is move the function definition inside the class definition. Notice the change in indentation.

class Time(object):
    def print_time(time):
        print(str(time.hour) + ":" + str(time.minute) + ":" + str(time.second))

Now there are two ways to call print_time. The first (and less common) way is to use function syntax:

>>> Time.print_time(start)
09:45:00

In this use of dot notation, Time is the name of the class, and print_time is the name of the method. start is passed as a parameter. The second (and more concise) way is to use method syntax:

>>> start.print_time()
09:45:00

In this use of dot notation, print_time is the name of the method (again), and start is the object the method is invoked on, which is called the subject. Just as the subject of a sentence is what the sentence is about, the subject of a method invocation is what the method is about. Inside the method, the subject is assigned to the first parameter, so in this case start is assigned to time.

By convention, the first parameter of a method is called self, so it would be more common to write print_time like this:

class Time(object):
    def print_time(self):
        print(str(time.hour) + ":" + str(time.minute) + ":" + str(time.second))

The reason for this convention is an implicit metaphor: The syntax for a function call, print_time(start), suggests that the function is the active agent. It says something like, “Hey print_time! Here’s an object for you to print.”

In object-oriented programming, the objects are the active agents. A method invocation like start.print_time() says “Hey start! Please print yourself.” This change in perspective might be more polite, but it is not obvious that it is useful. In the examples we have seen so far, it may not be. But sometimes shifting responsibility from the functions onto the objects makes it possible to write more versatile functions, and makes it easier to maintain and reuse code.

Exercise

def time_to_int(time):
    minutes = time.hour * 60 + time.minute
    seconds = minutes * 60 + time.second
    return seconds

def int_to_time(seconds):
    time = Time()
    minutes, time.second = divmod(seconds, 60)
    time.hour, time.minute = divmod(minutes, 60)
    return time

Write time_to_int as a method. It is probably not appropriate to rewrite int_to_time as a method; what object you would invoke it on?

Another example

Here’s a version of increment written as a method:

# inside class Time:

    def increment(self, seconds):
        seconds += self.time_to_int()
        return int_to_time(seconds)

This version assumes that time_to_int is written as a method, as in Exercise 1. Also, note that it is a pure function, not a modifier. Here’s how you would invoke increment:

>>> start.print_time()
09:45:00
>>> end = start.increment(1337)
>>> end.print_time()
10:07:17

The subject, start, gets assigned to the first parameter, self. The argument, 1337, gets assigned to the second parameter, seconds. This mechanism can be confusing, especially if you make an error. For example, if you invoke increment with two arguments, you get:

>>> end = start.increment(1337, 460)
TypeError: increment() takes exactly 2 arguments (3 given)

The error message is initially confusing, because there are only two arguments in parentheses. But the subject is also considered an argument, so all together that’s three.

The str method

str is a special method, like init, that is supposed to return a string representation of an object.

For example, here is a str method for Time objects:

# inside class Time:

    def __str__(self):
        return         print(str(time.hour) + ":" + str(time.minute) + ":" + str(time.second))

When you print an object, Python invokes the str method:

>>> time = Time(9, 45)
>>> print(time)
09:45:00

When I write a new class, I almost always start by writing init, which makes it easier to instantiate objects, and str, which is useful for debugging.

Exercise

Write a str method for the Point class. Create a Point object and print it.

Operator overloading

By defining other special methods, you can specify the behavior of operators on user-defined types. For example, if you define a method named add for the Time class, you can use the + operator on Time objects.

Here is what the definition might look like:

# inside class Time:

    def __add__(self, other):
        seconds = self.time_to_int() + other.time_to_int()
        return int_to_time(seconds)

And here is how you could use it:

>>> start = Time(9, 45)
>>> duration = Time(1, 35)
>>> print start + duration
11:20:00

When you apply the + operator to Time objects, Python invokes add. When you print the result, Python invokes str. So there is quite a lot happening behind the scenes! Changing the behavior of an operator so that it works with user-defined types is called operator overloading. For every operator in Python there is a corresponding special method, like add. For more details, see http://docs.python.org/2/reference/datamodel.html#specialnames.

Exercise

Write an add method for the Point class.

6.4

Inheritance

The language feature most often associated with object-oriented programming is inheritance. Inheritance is the ability to define a new class that is a modified version of an existing class.

It is called “inheritance” because the new class inherits the methods of the existing class. Extending this metaphor, the existing class is called the parent and the new class is called the child.

As an example, let’s say we want a class to represent a “hand,” that is, the set of cards held by one player. A hand is similar to a deck: both are made up of a set of cards, and both require operations like adding and removing cards.

A hand is also different from a deck; there are operations we want for hands that don’t make sense for a deck. For example, in poker we might compare two hands to see which one wins. In bridge, we might compute a score for a hand in order to make a bid.

This relationship between classes—similar, but different—lends itself to inheritance.

The definition of a child class is like other class definitions, but the name of the parent class appears in parentheses:

class Hand(Deck):
    """Represents a hand of playing cards."""

This definition indicates that Hand inherits from Deck; that means we can use methods like popcard and addcard for Hands as well as Decks. Hand also inherits __init from Deck, but it doesn’t really do what we want: instead of populating the hand with 52 new cards, the init method for Hands should initialize cards with an empty list.

If we provide an init method in the Hand class, it overrides the one in the Deck class:

# inside class Hand:

    def __init__(self, label=''):
        self.cards = []
        self.label = label
So when you create a Hand, Python invokes this init method:
>>> hand = Hand('new hand')
>>> print hand.cards
[]
>>> print hand.label
new hand

But the other methods are inherited from Deck, so we can use pop_card and add_card to deal a card:

>>> deck = Deck()
>>> card = deck.pop_card()
>>> hand.add_card(card)
>>> print hand
King of Spades

A natural next step is to encapsulate this code in a method called move_cards:

#inside class Deck:

    def move_cards(self, hand, num):
        for i in range(num):
            hand.add_card(self.pop_card())

move_cards takes two arguments, a Hand object and the number of cards to deal. It modifies both self and hand, and returns None. In some games, cards are moved from one hand to another, or from a hand back to the deck. You can use move_cards for any of these operations: self can be either a Deck or a Hand, and hand, despite the name, can also be a Deck.

Class diagrams

So far we have seen stack diagrams, which show the state of a program, and object diagrams, which show the attributes of an object and their values. These diagrams represent a snapshot in the execution of a program, so they change as the program runs.

They are also highly detailed; for some purposes, too detailed. A class diagram is a more abstract representation of the structure of a program. Instead of showing individual objects, it shows classes and the relationships between them.

There are several kinds of relationship between classes:

Objects in one class might contain references to objects in another class. For example, each Rectangle contains a reference to a Point, and each Deck contains references to many Cards. This kind of relationship is called HAS-A, as in, “a Rectangle has a Point.” One class might inherit from another. This relationship is called IS-A, as in, “a Hand is a kind of a Deck.” One class might depend on another in the sense that changes in one class would require changes in the other. A class diagram is a graphical representation of these relationships. For example, Figure 6.1 shows the relationships between Card, Deck and Hand. !(Class Diagram)[http://www.greenteapress.com/thinkpython/html/thinkpython026.png] Figure 6.1: Class diagram. The arrow with a hollow triangle head represents an IS-A relationship; in this case it indicates that Hand inherits from Deck. The standard arrow head represents a HAS-A relationship; in this case a Deck has references to Card objects.

The star (*) near the arrow head is a multiplicity; it indicates how many Cards a Deck has. A multiplicity can be a simple number, like 52, a range, like 5..7 or a star, which indicates that a Deck can have any number of Cards.

A more detailed diagram might show that a Deck actually contains a list of Cards, but built-in types like list and dict are usually not included in class diagrams.

Exercise 4

Read TurtleWorld.py, World.py and Gui.py and draw a class diagram that shows the relationships among the classes defined there. 18.9 Debugging

Inheritance can make debugging a challenge because when you invoke a method on an object, you might not know which method will be invoked.

Suppose you are writing a function that works with Hand objects. You would like it to work with all kinds of Hands, like PokerHands, BridgeHands, etc. If you invoke a method like shuffle, you might get the one defined in Deck, but if any of the subclasses override this method, you’ll get that version instead.

Any time you are unsure about the flow of execution through your program, the simplest solution is to add print statements at the beginning of the relevant methods. If Deck.shuffle prints a message that says something like Running Deck.shuffle, then as the program runs it traces the flow of execution.

As an alternative, you could use this function, which takes an object and a method name (as a string) and returns the class that provides the definition of the method:

def find_defining_class(obj, meth_name):
    for ty in type(obj).mro():
        if meth_name in ty.__dict__:
            return ty
Here’s an example:
>>> hand = Hand()
>>> print find_defining_class(hand, 'shuffle')
<class 'Card.Deck'>

So the shuffle method for this Hand is the one in Deck. find_defining_class uses the mro method to get the list of class objects (types) that will be searched for methods. “MRO” stands for “method resolution order.”

Here’s a program design suggestion: whenever you override a method, the interface of the new method should be the same as the old. It should take the same parameters, return the same type, and obey the same preconditions and postconditions. If you obey this rule, you will find that any function designed to work with an instance of a superclass, like a Deck, will also work with instances of subclasses like a Hand or PokerHand.

If you violate this rule, your code will collapse like (sorry) a house of cards.